정리 : Autoencoder
이번 포스트는 Autoencoder 입니다. 데이터 압축을 목적으로 사용되기 시작해서 생성, 변환 등 다양한 목적에 활용되고 있는 Autoencoder의 종류에 대해 정리해보았습니다.
Autoencoder
Autoencoder는 high-dimensional data를 보다 저차원으로 압축하기 위한 모델입니다.
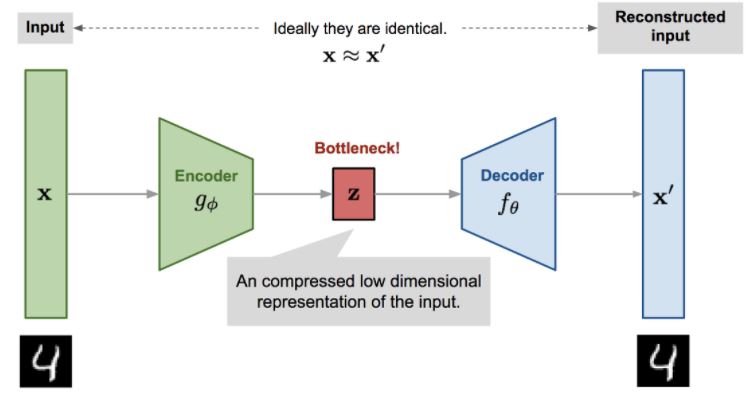
압축을 위한 구조로 neural network를 사용하고 학습을 위한 target을 설정하기 위해 reconstruction을 수행하는 decoder 구조를 bottleneck layer 뒤에 추가하게 됩니다. 데이터 압축, 주요 feature 추출을 위한 방법으로 PCA가 많이 알려져 있는데, Autoencoder의 neural network 구조에서 non-linearlity를 학습할 수 있게하는 activation function(ex. relu, sigmoid)부분을 제외하면 실제로 PCA와 비슷한 결과를 보여준다고 합니다.
Denoising Autoencoder
Identity function을 학습하는 Autoencoder는 overfitting의 우려가 크기에 제안된 것이 Denoising Autoencoder 입니다.
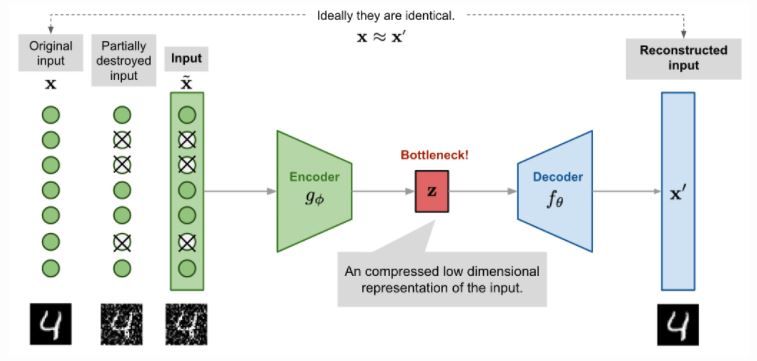
Denoising Autoencoder는 input의 임의의 영역을 noise로 바꾸고, reconstruction은 noise의 영역까지 원본처럼 복원할 수 있도록 학습합니다. 일부 노드를 지우는 것으로 생각하면 dropout과 같은 개념으로 생각할 수 있지만 dropout paper보다 4년이나 먼저 나온 연구라고 하네요.
Sparse Autoencoder
Sparse Autoencoder는 autoencoder의 hidden layer에 sparsity 조건을 추가한 것으로 생각할 수 있습니다. sparsity 조건이란 hidden unit의 activation을 제한하는 것인데, 이를 통해 hidden unit의 수가 커져도 좀 더 의미 있는 feature를 학습하는 것이 가능해집니다. Sparse Autoencoder 중 대표격인 k-Sparse Autoencoder의 결과를 보겠습니다.

k-Sparse Autoencoder는 hidden layer의 activation 값 중 가장 큰 k개의 값만 사용합니다.
k 값이 작아질수록 적은 정보로 reconstruction을 수행해야 하기에 hidden layer에서는 점점 high level feature를 학습하게 됩니다.
Convolutional Autoencoder
Autoencoder는 정형, 비정형(언어, 이미지 등) 등의 모든 데이터에 대해 사용할 수 있지만, 이미지 데이터에 대해 Autoencoder를 사용할 땐 보통 Convolutional Autoencoder를 기본으로 생각합니다. CAE는 이전까지 input을 flatten해서 사용하던 방식에 CNN을 추가한 것입니다. 이로써 parameter 수를 줄여 좀 더 큰 이미지에도 사용할 수 있고, convolution 단위로 좀 더 의미있는 feature를 학습할 수 있다는 점 등 CNN의 기본적인 장점을 얻게되는 효과가 있습니다.
Variational Autoencoder
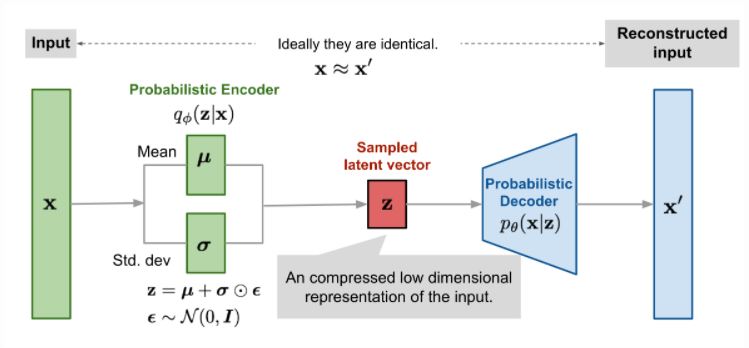
Variational Autoencoder는 Autoencoder 구조에서 latent variable z를 얻기위한 trick과 loss에 KL divergence가 추가된 것인데요. 이렇게 표면적으로는 Autoencoder에 일부 개념이 추가된 것으로 보이지만 목적 자체가 Autoencoder와는 다르기에 전혀 다른 모델로 구분되곤 합니다. 앞서 언급했던 것처럼 Autoencoder는 데이터 압축, 즉 특정 maniflod를 학습하기 위한 모델인 반면, VAE는 GAN처럼 Generative model로 분류됩니다.
ELBOW
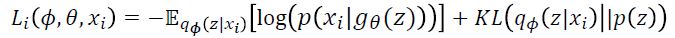
VAE의 Loss는 위와 같이 정의되고 이를 유도할 때 보통은 log likelihood를 maximize 하는 식에서 출발하는 데,
개인적으로 이상적인 sampling 함수에 실제 sampling 함수를 근사시키는 term에서 출발하는 것이 좀 더 이해하기 쉬운 것 같습니다.
먼저, Generative model이라고 했으니 vector z에서 x를 생성하는 것으로 생각하고 x의 distribution을 encoding vector를 활용하여 다음과 같이 나타냅니다.
@@ p_{\theta}(x^{(i)}) = \int p_{\theta}(x^{(i)}|z)p_{\theta}(z)dz @@
여기서 모든 가능한 z의 분포에 대해 계산할 수 없기에, neural network 형태의 encoder가 등장하게 됩니다.
z를 다루기 쉬운 normal distribution으로 가정하고, x를 input으로 하는 이상적인 sampling 함수 $q_{\phi}(z|x)$를 정의하는 것입니다.
그리고 이 sampling 함수(이상적인)와 $p_{\theta}(z|x)$ 사이의 KL divergence를 minimize하는 것으로 목적함수를 정의합니다.
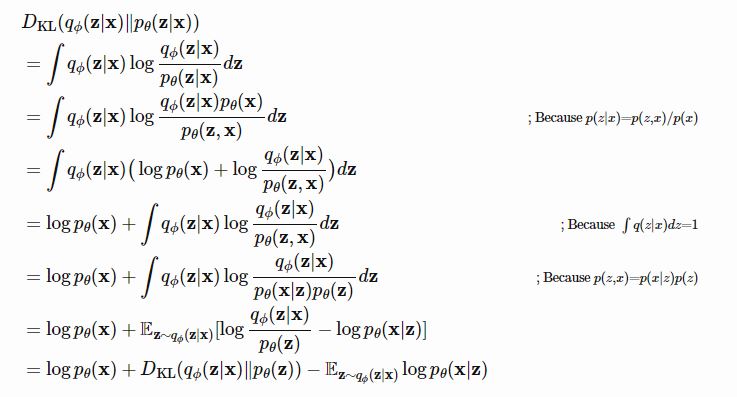
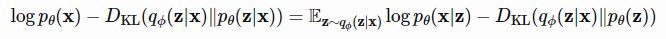
이렇게, 출발은 달랐지만 결국 $\textbf{log} p_{\theta}(x) $ 가 포함된 식이 유도되었고,
이상적인 sampling 함수 $q_{\phi}(z|x) $ 가 포함된 term은 직접 계산할 수 없기에,
$\textbf{log} p_{\theta}(x) $ 의 lower bound(ELBO)가 VAE의 Loss가 됩니다.
Reparameterization Trick
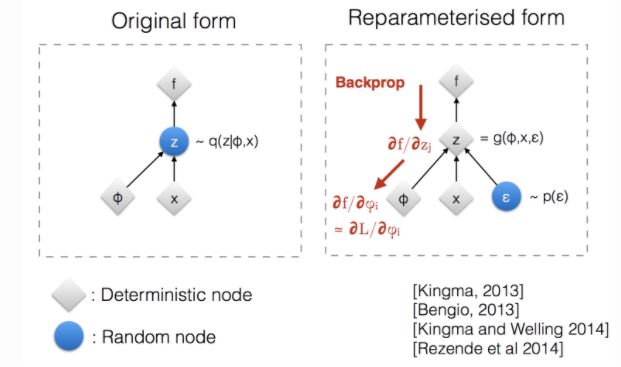
encoder를 sampling 함수로 사용하여 z를 sampling하는 부분은 backpropagation 식을 정의 할 때 문제가 될 수 있는데,
VAE에선 이 부분을 간단한 trick으로 해결합니다.
위 그림처럼 normal distribution에서 sampling한 $\epsilon \sim N(0,1) $ 값과 encoder의 output을 연산하여 z를 계산하게 하는 것으로 backpropagation에 문제가 없게 하였습니다.
이렇게 정의된 VAE는 여러 다양한 task 들에서 활용도가 높지만 단순히 Generative model의 성능 면에서는 GAN에 비해 뛰어나지 못하다는 단점이 있습니다. 특히, output 이미지가 전체적으로 blurry한 경향을 보이는데, 이는 Loss에 사용된 MSE term 의 한계로 볼 수 있습니다.
Reference
Lil’log : From Autoencoder to Beta-VAE
라온피플 : 머신러닝 학습 방법(part 14) - AutoEncoder(5)
라온피플 : 머신러닝 학습 방법(part 14) - AutoEncoder(6)
Jeremy Jordan : Variational autoencoders
Steve-Lee’s Deep Insight : [정리노트] [AutoEncoder의 모든것] Chap4. Variational AutoEncoder란 무엇인가(feat. 자세히 알아보자)