NeRF : Neural Radiance Field(1)
이번 포스트에선 2020년 이후 Computer vision 분야에서 3D view synthesis를 인기 연구주제로 자리잡게 한 NeRF 논문을 포함하여 NeRF와 관련된 연구들을 정리해보았습니다.
NeRF : Representing Scenes as Neural Radiance Fields for View Synthesis
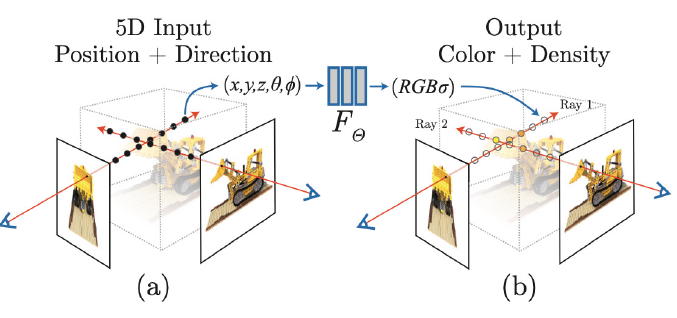
NeRF는 3D view를 생성하는 task를 수행하고 같은 물체를 다양한 시점에서 찍은 이미지가 있을 때, 이 중 일부를 학습에 사용하고 나머지로 평가하는 방식을 주로 사용합니다. 즉, 주어진 view를 학습하여 novel view를 생성할 수 있는 모델을 학습한다고 할 수 있습니다.
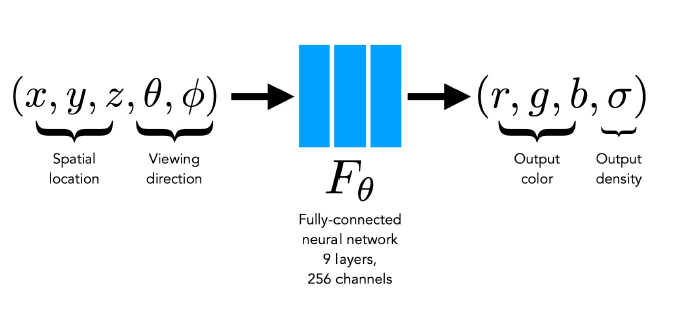
NeRF는 3D 위치정보(Spatial location)와 물체를 바라보는 방향(Viewing direction)을 입력으로 받아, 색상과 density를 예측할 수 있는 fully-connected network를 학습합니다. density는 투명도의 역수 개념으로,
density가 낮다 = 투명하다 or 뒤에 있는 것들이 잘 보인다.
density가 크다 = 뒤에 있는 것들이 가려진다.
로 해석할 수 있습니다.
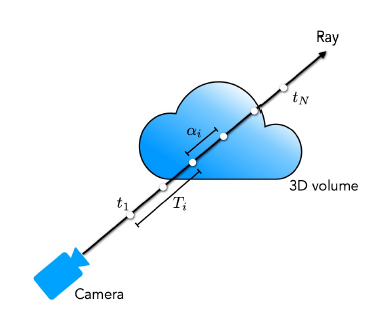
카메라 위치에서 3D 물체의 한 지점을 바라볼때 생기는 직선을 Ray 라고 합니다.
카메라 위치(o)와 viewing direction(d)이 정해지면 Ray 위에 있는 3d point들의 좌표는 t값에 대해 다음 식을 통해 계산할 수 있습니다.
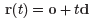
ray에 있는 점들이 가지는 color 값들을 weighted sum하면 카메라 위치에서 바라봤을 때 보이는 2d 이미지 상에서 하나의 픽셀이 가지는 color 값을 구할 수 있고, 이를 식으로 나타내면 다음과 같습니다.
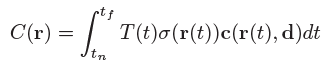
r은 ray 하나를 의미하고, $t_n, t_f$는 각각 ray가 물체를 통과할때 시작점과 끝점을 의미합니다. c와 $\sigma$는 각각 t지점에서의 color값과 density입니다. density가 클수록 t지점에서의 색상이 투명하지 않고 진하다는 것을 의미하여 색상에 가중치를 크게 주는 것으로 해석할 수 있습니다.
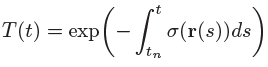
$T(t)$는 위와 같이 $\sigma$에 대한 적분을 통해 구하는데, 이는 t보다 앞에 있는 점들의 density합으로 생각할 수 있습니다. 이 값이 크면 앞에 있는 것에 가려져 잘 보이지 않기 때문에 마이너스 부호가 붙어 있는 모습입니다. 즉, t보다 앞부분의 density가 작을수록, t지점의 density가 클수록 t지점에서의 색상값에 곱해지는 weight는 커지게 됩니다.
논문에선 ray를 통해 본 색상 정보를 위의 식들처럼 continuous한 함수를 직접 적분해서 구하는 것이 아닌 ray 위의 점들을 샘플링해서 사용합니다. 샘플링은 아래와 같이 uniform 분포에서 진행합니다.
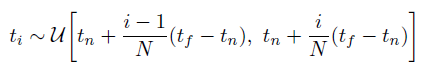
discrete하게 변형하고 나면 아래와 같이 식이 바뀌고 이 식에 있는 $\sigma, c$를 neural network를 통해 구하게 됩니다.
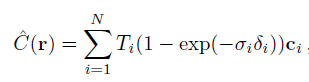
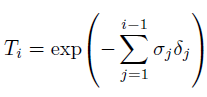
여기까지의 과정을 보면 network 하나만 필요할 것 같지만, 사실 논문에선 두 개가 사용됩니다. 둘은 각각 coarse와 fine한 정보를 위한 것이고 t를 샘플링하는 방법에서 차이 가 있습니다. coarse network는 위의 설명처럼 uniform하게 sampling하여 학습하고, 이렇게 sampling된 점들을 coarse network에 통과시켜 얻은 weight 값을 확률 분포로 사용하여 다시 한 번 sampling하고 이 점들은 fine network의 학습에 사용됩니다.
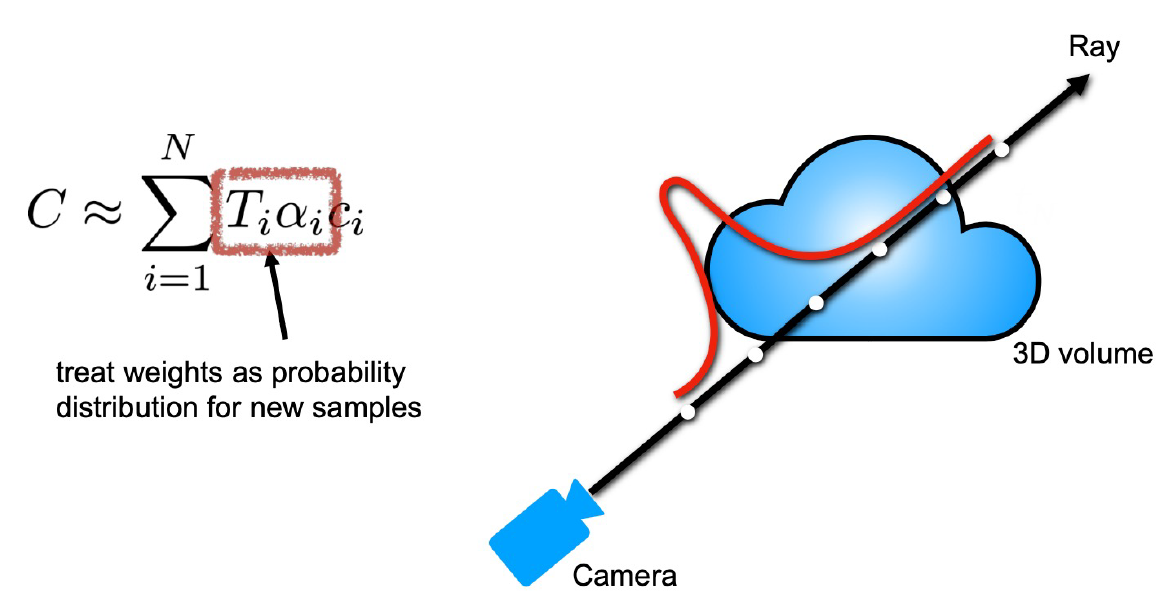
이러한 과정은 ray 위의 점들을 sampling할 때 좀 더 의미있는 점들을 찾기 위해 coarse network를 일종의 teacher모델 처럼 사용하는 것으로 생각할 수 있습니다. 결국 loss 함수는 아래와 같이 두 network에 대한 식으로 구성됩니다.
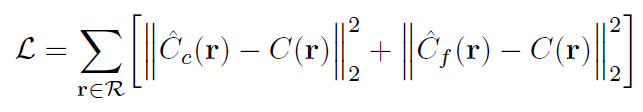
아래는 NeRF에서 사용한 FC network의 구조입니다.
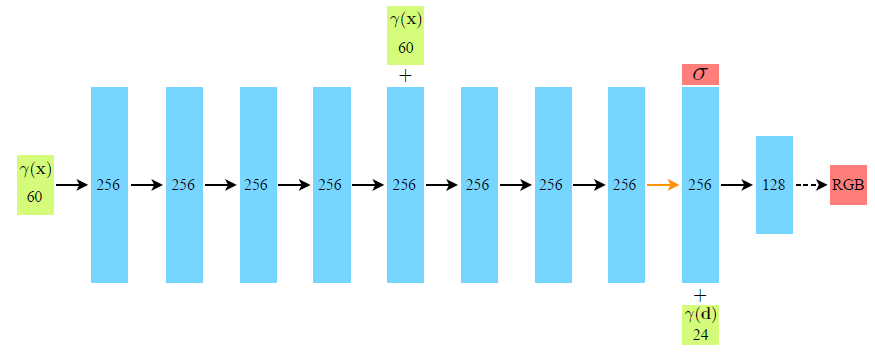
$\gamma(\mathrm{x})$ : 3d point의 위치, $\gamma(\mathrm{d})$ : viewing direction
network 중간에 한 번 더 더해지는 $\gamma(\mathrm{x})$는 skip connection을 의미합니다.
구조를 보면 처음엔 입력으로 카메라 위치만 사용해서 density $\sigma$를 구하고 density와 viewing direction을 같이 입력으로 사용해서 최종 rgb 값을 구하는 것을 볼 수 있습니다. 즉 density는 바라보는 방향과 상관없이 일정하고, 색상은 바라보는 방향에 따라 달라진다는 가정이 있는 것으로 보입니다.
입력 dimension이 60d, 24d인 것은 positional encoding을 사용했기 때문입니다.
좌표 기반의 저차원 입력값을 고차원 공간에 매핑할 때, NN에 들어가기 전 high frequency functions을 사용해주면 효과적이라는 이전 연구결과를 사용했다고 합니다.
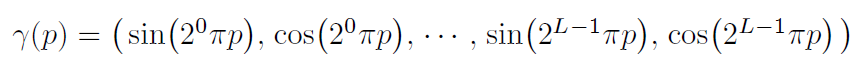
positional encoding엔 위와 같이 sin, cos 함수가 사용되고, 결과적으로 dimension이 2L 배가 된다.
바라보는 방향보다 3d point의 위치에 정보가 더 많기 때문에 position에는 L=10을 사용하고 바라보는 방향에는 L=4를 사용합니다.
여기서, positional encoding까지 생각하면 spatial location은 3d에서 20배인 60d가 되는 것을 이해할 수 있는데 viewing direction은 2d에 8배를 해도 16d라 위 그림과 맞지 않습니다. 이 부분은 사실 3차원 공간이기 때문에 바라보는 방향도 x,y,z의 좌표가 있는 3d가 맞고 이렇게 생각하면 위 그림처럼 24d가 되는 것으로 생각할 수 있습니다. viewing direction을 2d라고 한 것은 카메라는 물체가 있는 방향을 바라봐야 하기 때문에 3d 중 하나의 좌표가 나머지 두 개로 나타낼 수 있기 때문으로 생각됩니다.
Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains
이 논문은 NeRF에서 생성되는 view의 detail한 부분을 더 잘 생성해내는 논문입니다.

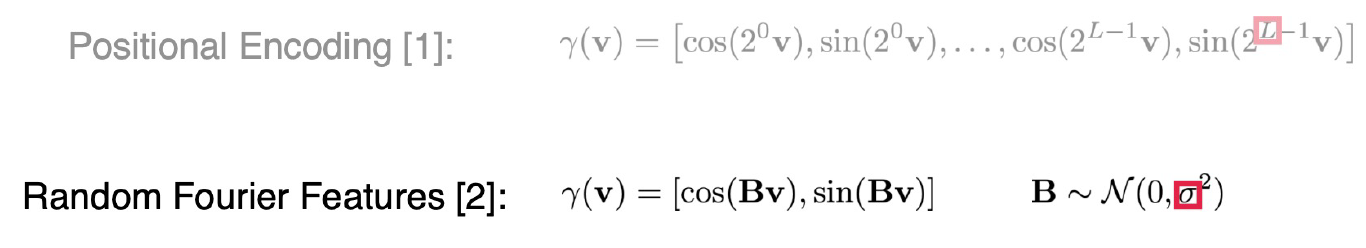
NeRF에서 사용한 Positional Encoding을 위와 같이 Random Fourier Features 형태로 변경했고, 2의 거듭제곱 모양이 곱해지는 부분에 normal분포에서 sampling된 B가 사용됩니다.
논문의 contribution은 다음 두 가지로 정리할 수 있습니다.
*Fourier feature mapping은 positional encoding과 같은 형태를 말힙니다.
- 좌표를 입력으로하는 MLP가 빠질 수 있는 spectral bias를 극복하는데 Fourier feature mapping이 사용될 수있음을 Neural Tangent Kernel이론과 간단한 실험을 통해 보였다.
- 적절한 $\sigma$를 선정하여 Random Fourier feature mapping을 사용하면 성능을 더 개선할 수 있다.
Reference
paper :
NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains
other :
PR-302: NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
[Seminar] NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis
Lecture8 AAA738 SeungryongKim