GAN의 학습은 Generator와 Discriminator를 반복하여 학습해야 되기에 각각의 학습 횟수에 따라 mode collapse 등의 문제가 발생하기 쉽다는 불안정성을 가지고 있습니다. 이 논문은 cost function을 변경하는 것으로 이러한 GAN 학습의 불안정성을 개선하였다는 점에서 GAN 발전에 기여도가 높다고 볼 수 있습니다.

Introdunction

확률분포를 학습한다는 것은 확률밀도를 정의하고 real data에 대해 확률 값을 최대화하는 문제를 푸는 것으로 접근할 수 있고, 확률 값을 최대화 하는 문제는 식으로 나타내면 다음과 같습니다.

@@ \underset{\theta\in \mathbb{R}^{d}}{max}\frac{1}{m}\sum_{i=1}^{m}\log P_{\theta}(x^{(i)}) @@

이 식은 실제 데이터의 분포 $P_{r}$ 이 확률밀도함수 $P_{\theta}$를 따른 다고 가정하면 Kullback-Leibler divergence 를 최소화 하는 것으로 풀 수 있습니다.

@@ \min \text{KL} (P_{r} \parallel P_{\theta}) @@

GAN의 학습을 위해 항상 KL divergence를 사용해야하는 것은 아니지만 일반적인 GAN의 loss함수는 아래와 같은 형태입니다.

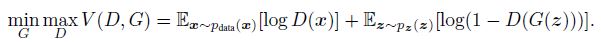
GAN_loss

이 식은 최적의 discriminator에 대한 generator의 식으로 바꾸면 Jensen-Shannon distance를 최소화하는 식이 됩니다. (식 유도는 GAN paper 참조)

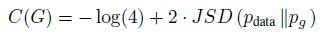
GAN_loss2

위와 같이 GAN loss는 JS distance를 포함하고 있기에 mode collapse나 adversarial training 과정에서 오는 학습의 불안정성 등 여러가지 단점을 가지고 있습니다. 이 논문에선 실제 데이터와 생성 데이터의 분포 사이의 새로운 distance metric, EM distance를 제안함으로써 이러한 문제들을 해결했다고 합니다.

Different Distances

두 확률분포 사이의 거리 metric은 다음과 같은 것들이 있습니다.

Different_Distances

먼저, TV는 두 분포의 측정값의 거리 중 최대값을 의미합니다.

TV

KL divergence는 두 분포의 차이를 계산할 때 많이 사용되는 metric이지만, input으로 들어가는 두 분포의 순서에 따라 값이 달라지기에 distance를 나타내기엔 적절하지 않습니다. 그래서 KL divergence를 응용한 것이 Jensen-Shannon distance 입니다.

KL_JS

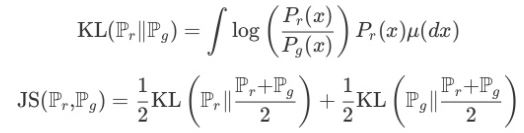
하지만, 이러한 기존의 distance들은 다음과 같은 문제점을 가지고 있습니다.

  • Saturated gradients
  • 비교하는 두 분포에 의미 있는 intersection이 없을 경우 학습이 잘 되지 않는다.
  • Mode collapse : discriminator를 속일 수 있는 특정 이미지만 generator에서 생성하게 됨
  • Unstable : generator, discriminator의 adversarial training이 어려움

그리고 이러한 문제점을 보완한 것이 바로 이 논문에서 제시한 EM(Earth Mover) distance 입니다.

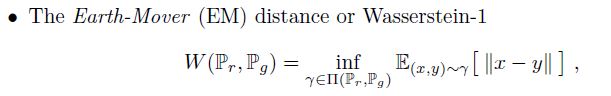
EM_dist

식은 복잡하게 되어 있지만 위 식은 $P_{r}$을 $P_{g}$로 옮길 때 드는 최소한의 비용을 의미합니다.

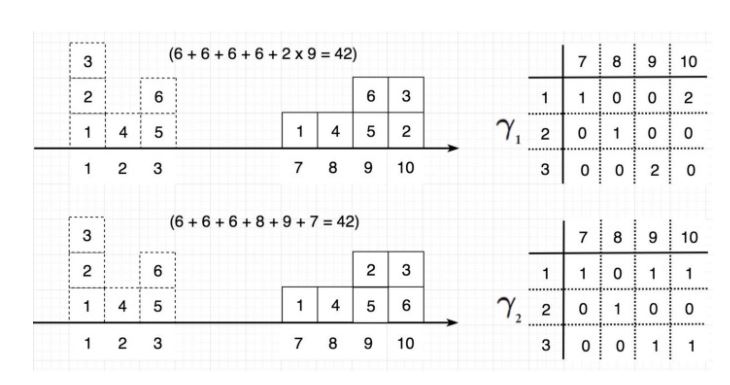
EM_dist_example

그럼, EM distance가 기존과 어떤 차이가 있는지 보겠습니다.
uniform distribution을 따르는 $Z \sim U[0,1]$에 대해 두 확률분포 $P_{0}$, $P_{\theta}$를 다음과 같이 정의하겠습니다.
@@ P_{0} = (0, Z) \in \mathbb{R}^{2} @@ @@ P_{\theta} = (\theta, Z) \in \mathbb{R}^{2} @@

그럼, 위에서 정의한 4가지 distance metric으로 두 확률분포 사이 거리를 계산해보겠습니다.

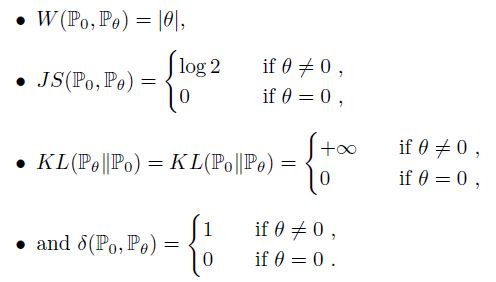
dist_example

Wasserstein distance(EM distance)를 제외한 다른 metric은 모두 $\theta=0$ 에서 continuous하지 않습니다. 이 말은 gradient값 또한 continuous하지 않다는 것이고, 확률분포 $P_{\theta}$를 $P_{0}$에 가깝게 학습할 수 없다는 뜻이 됩니다.
이 예에서는 학습해야 하는 분포와 target 분포 사이의 intersection이 없는 상황을 가정했는데, 실제로 generator 학습 초기에는 real data와 전혀 상관없는 이미지가 생성되기에 이런 상황은 자주 일어난다고 볼 수 있습니다. 즉, 다른 metric과 달리 항상 유의미한 distance값을 가지는 EM distance가 이론적으로도 적절한 metric이라고 할 수 있습니다.

Train

EM distance가 확률분포를 학습할 때 유의미하다는 것은 알았지만 infimum을 구하는 문제는 실제 neural network로 구현하기 어려움이 있습니다. 논문에선 이 부분을 해결하기 위해 Kantorovich-Rubinstein duality를 이용하여 Wasserstein distance를 아래와 같이 정의합니다.

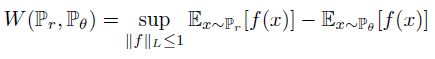
W_dist

논문에서 Theorem 1~3을 통해 Wasserstein distance의 연속성과 미분가능성, 분포의 수렴성, gradient의 형태 등에 대해 증명하고 있는데, 이 부분을 모두 커버하긴 어려움이 있기에 이 페이지에선 infimum값을 계산해야하는 EM distance 식이 Kantorovich-Rubinstein dualtiy를 이용하면 아래와 같이 maximum 값을 해결하는 것으로 바뀌고, 이 때 1-Lipschitz로 f를 제약한다 정도로 정리하겠습니다. (자세한 설명은 링크를 참고하시기 바랍니다.)

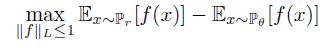
W_dist2

학습 알고리즘에서 특이한 점은 discriminator를 논문에선 critic으로 명명하며, generator와 discriminator를 비슷하게 학습했던 일반적인 GAN과 달리 w-gan의 학습은 critic을 5번 학습하고 generator를 한 번 학습한다는 점입니다. 또한, Lipschitz condition으로 critic을 제한하기위해 weight clipping이라는 단순한 방법을 사용하는데, w-gan의 문제는 많은 부분 여기서 발생하게 됩니다. 후속 논문에서 간단한 loss term을 추가하는 것으로 이 문제를 해결하였고 해당 논문도 Reference에 추가하였으니 참고하셔도 좋을 것 같습니다.

algorithm

Results

마지막으로 w-gan의 학습 결과와 conclusion에 대해 간단하게 정리하였습니다.

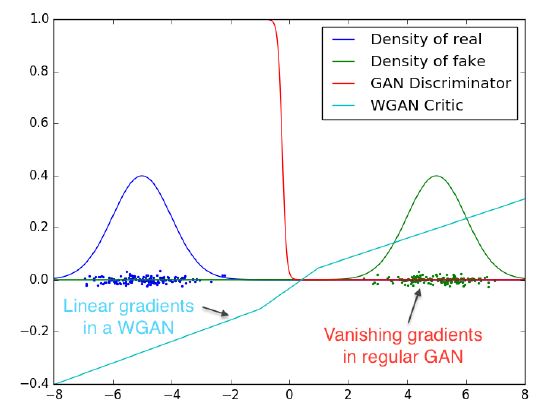
gradient_graph

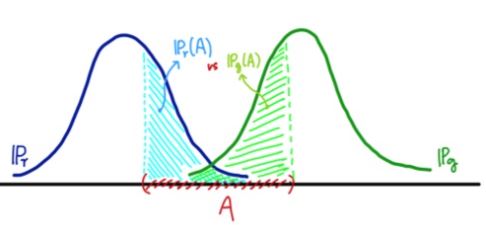
위 그림은 Gaussian 분포를 두 개 정의하였을 때, 일반적인 GAN과 W-GAN의 gradient의 차이에 대해서 보여주고 있습니다. 두 분포의 intersection이 없을 때, 일반적인 GAN은 vanishing gradients 문제가 발생하지만 W-GAN은 모든 구간에서 유의미한 gradient값을 가지고 있습니다.

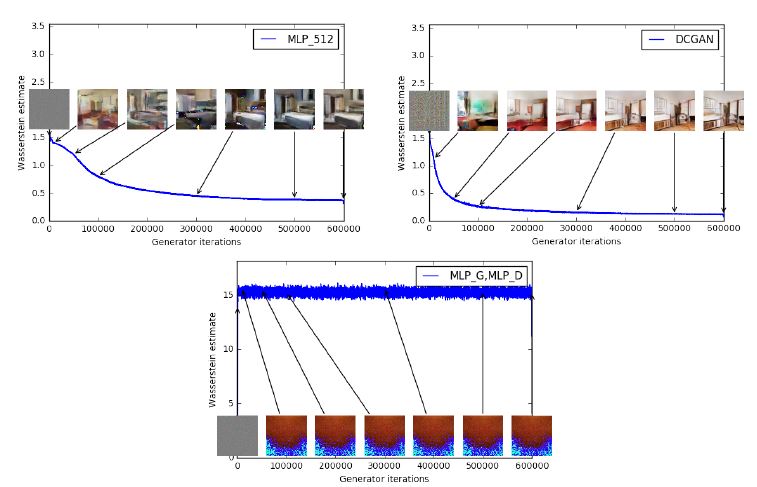
result_graph

wasserstein distance는 또한, GAN의 성능 평가 지표로도 유의미합니다. 위 첫번째와 두번째 그림은 각각 MLP와 DCGAN으로 학습하였을 때, iteration이 진행됨에 따라 wasserstein distance의 변화를 보여줍니다. distance 값이 작아질 수록 육안으로도 이미지가 잘 생성되었음을 확인할 수 있습니다. 반면, 세번째 그림은 학습이 잘 되지 않은 GAN의 경우 wasserstein distance값도 크게 변화가 없는 것을 볼 수 있습니다.

Conclusion

  • 새로운 distance metric의 정의하여 train 과정의 안정성을 높였다.
  • mode collapse 문제를 해결하였다.
  • loss 값이 생성된 이미지의 평가 지표로도 유용하다.
  • Adam 같은 momentum-based optimizer가 잘 동작하지 않아 학습 속도가 느리다는 단점이 있다.

Reference

paper :
GAN : https://arxiv.org/abs/1406.2661
Wasserstein GAN : https://arxiv.org/abs/1701.07875
Improved Training of Wasserstein GANs : https://arxiv.org/abs/1704.00028

etc :
https://www.slideshare.net/ssuser7e10e4/wasserstein-gan-i
https://www.youtube.com/watch?v=tKQwlf-DAl0
https://jonathan-hui.medium.com/gan-wasserstein-gan-wgan-gp-6a1a2aa1b490
https://www.youtube.com/watch?v=gPDShRk3odk
https://vincentherrmann.github.io/blog/wasserstein/